USING POWER MOSFETs to Drive Resonant Transformers

Gary L. Johnson, Ph.D.

Introduction

The most common way of supplying power to a Tesla coil or resonant transformer is through a spark gap.  A fixed gap is used for smaller sizes, while a rotating mechanical commutator is used with the larger sizes.  These certainly do their job, but have some disadvantages.  One is the sparking during operation.  Any electrical discharge will dissipate energy in the form of heat, light, and chemical energy.  The breakdown voltage and the amount of energy transferred are difficult to maintain at constant values as atmospheric conditions change and as the stationary gap or commutator becomes worn or dirty.  Another disadvantage is that gaps require operation at nearly full power, even while a new system is being tested and tuned.

Vacuum tube drivers have been used in the past for small systems.  Today, power MOSFETs can be used to drive small demonstration units or to help tune the larger units before they are operated at full power.  This paper is an introduction to the topic.

MOSFET Theory

Power MOSFETs (Metal Oxide Semiconductor Field Effect Transistor) are widely used in switching power supplies.  The symbol for an N channel device is shown in Figure 1. When no voltage is applied between the gate G and the source S, there will be no path or channel between the drain D and the source.  The device acts like an open switch.  When the gate is made several volts positive with respect to the source, a channel is produced and current can flow from D to S.  The diode in the symbol is produced by the manufacturing process for power MOSFETs but not for small signal MOSFETs). Therefore the power MOSFET is basically a high speed switch in parallel with a diode.  The diode has the characteristics of a fast recovery diode.

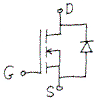
Figure 1. N channel device symbol.

Power Ratings

A wide variety of power MOSFETs are commercially available.  The IRF82O, for example, is rated at 500V, 2.5A continuous or 10A pulse, and a resistance of 3 ohms between drain and source when on.  The cost is slightly over a dollar in small quantities. The IRF640 is rated at 200V, 18A continuous or 72A pulse, with an on resistance of 0.18 ohms.  The cost is about four times that of the IRF820.  It is possible to get power MOSFETs with rated voltages up to 1000V.  Higher voltages can be obtained by connecting the power MOSFETs in series.

These power levels are not trivial.  If we operate at 150V and 18A, the power being supplied is (150)(18) = 2700W. This should drive a small Tesla coil in a very satisfactory manner.

After burning up a dozen or so MOSFETs, I learned that the current ratings listed require very special heat sinking to get even close to the specification.  The power dissipated in the IRF640 at 18A is I²R = (18)²(0.18) = 58W in a device with about the volume of a 5 W resistor.  A large heat sink is essential.  Even with a good heat sink, I would not suggest exceeding 6 to 8A with the IRF640 unless a good fan is also available.

A good power MOSFET shows a very high resistance between any pair of leads, except when the diode test function of the multimeter is used between the source and drain.  Most failures that I observed had at least one pair of terminals shorted together.

Electrical Isolation

The logical place to put the MOSFET in the circuit is between the high voltage terminal of the supply and the high voltage terminal of the load.  This means that when the MOSFET is conducting, both S and D are above ground.  Therefore the gate circuit must be operated without any ground connection.  One way of obtaining this isolation is to use optoisolators and a local 9V battery to supply the gate voltage.  The optoisolator that I selected is the H11L3, which has the circuit shown in Figure 2.  When a few milliamperes of current are supplied to the light emitting diode (LED) by a function generator or other source of pulses, the Schmidt trigger output of the optoisolator drops from logic high to logic low.  The electrical isolation between the LED and the Schmidt trigger is 2500V(rms), more than adequate for most tests.  The equivalent optoisolator made by Motorola has an isolation of 7500V, so higher values are available if needed.

The optoisolator circuit is shown in Figure 3.  The function generator circuit supplies a pulse train through a coaxial cable and current limiting resistor R, to the LED.  R, should be selected to allow adequate current to the LED, but without overloading the function generator.  For example, suppose the lowest voltage expected at the optoisolator end of the cable is 7V.  The LED voltage would not be more than about 1V, so R₁ needs to drop about 6V.  The specification for the H11L3 is that it will change state for not more than 5mA of LED current.  By measurement, the highest LED current required for a group of 10 chips was 1.84 mA.  Rounding this off to 2 mA allows us to select R, = 6/2 = 3k ohms.  If the source is not current limited, a value closer to 1k ohm might be better.

Power is supplied to the Schmidt trigger portion of the optoisolator and to the gate of the power MOSFET by a 9V battery, with a switch to conserve battery life when the circuit is not in use.  The 270 ohm resistor is a pullup resistor required by the Schmidt trigger output.  We want a noninverted output so we connect the gate to +9V rather than connect the source to -9V.  When pin 4 goes low with respect to pin 5, at the same time it goes high (actually inverted high) with respect to pin 6.  This will put nearly 9 V on the gate with respect to the source, more than enough to fully turn on the power MOSFET.

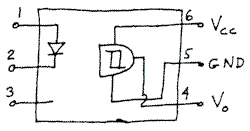
Figure 2 - Schematic of the H11L3 optoisolator IC.

Figure 3 - Circuit utilizing the H11L3 optoisolator IC.

Switching Speeds

This optoisolator is rated for a supply voltage between 3 and 16V, so the 9V battery is well within the operating range.  Its maximum switching speed is 1 MHz in a non return to zero logic system.  The highest speed I have been able to get is about 300 kHz, which is still far above the switching speed of a mechanical commutator.

With a different optoisolator, the MOSFET could supposedly switch at still higher speeds.  The sum of the turn-on delay time, the rise time, the turn-off delay time and the fall time is 230ns for the IRF640 under specified test conditions.  This would yield an absolute maximum switching speed of 4.35 MHz.  This can be misleading because it is only possible with a very low function generator impedance, so the gate to source capacitance can be charged and discharged quickly.  With a generator impedance of 50 ohms, rather than the 4.7 ohms specified in the test, the switching time increases by at least a factor of three [1].  Therefore, if switching speeds much faster than 300 kHz are required, a different optoisolator would be required, and possibly a buffer acting as a low output impedance gate driver.

Using an optoisolator allows the power MOSFET to be mounted very near the coil under test, but with the function generator and other test equipment in a shielded environment some distance away.  The Schmidt trigger output will help shape the pulse being input to the gate if the rise and fall times of the function generator output are not very fast.  The optoisolator and power MOSFET should be shielded in the presence of high electric and magnetic fields, at least in an aluminum box.

Application Circuit

The basic circuit for applying pulses to a coil is shown in Figure 4.  The diode D, provides a path for current to flow from the inductive coil when the MOSFET is turned off.  It should be of the fast recovery type [such as FR 304].  At low frequencies, the coil will appear as an inductor, with the current shown in Figure 5.  At resonance, the output voltage of the coil is nearly sinusoidal, which requires a sinusoidal input current, as shown in Figure 6.  The resistor R, is chosen to force the decay portion of the cycle to be approximately the same length as the rise portion.  This helps the current to become sinusoidal as resonance is approached.  Note that we can have a sinusoidal current even while applying what is basically a square wave voltage.

Mid-frequency Model

A coil of wire behaves as an inductor only at low frequencies, well below the operating frequency of a resonant transformer.  At frequencies of interest, it really needs to be treated as a distributed circuit, or a type of transmission line [2]. This analysis is not easy, and requires a good background in electromagnetic theory.  A less sophisticated approach which helps explain some of the phenomena is to consider a lumped model such as Figure 7.  The coil has interwinding capacitances, which are shown in the figure as a lumped capacitor C_L.  The diode has stored charge in the reversed biased mode which must be removed before it can conduct in the forward direction.  This can be represented by C_D.  At the instant the MOSFET is switched off, C_D would be charged to the supply voltage V_B.  C_M is the capacitance between drain and source of the MOSFET.  It would be uncharged at the instant the MOSFET is turned off.

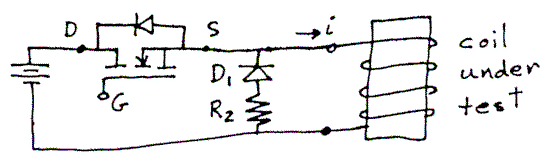
Figure 4 - Pulse application circuit for coil.

Figure 5 - Current in coil at low frequencies.

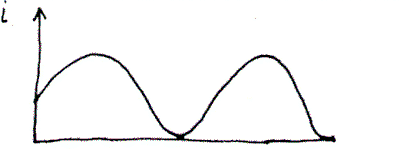
Figure 6 - Current in coil at resonant frequencies.

At the instant of MOSFET turnoff, there is a current i_L flowing, which cannot change magnitude instantly because of the inductance.  However, it starts to decrease according to V_L = L di/dt.  This current is being supplied by the discharging currents from C_D and C_L and the charging current through C_M.  The inductor and these three capacitors form a resonant circuit.  The voltage across C_L goes to zero while current is still flowing down in the inductor and then becomes negative as the bottom plate of C_L is positively charged by i_L.  At a later time, i_L will become zero, and all the initial energy is stored in the capacitors.  The capacitors then start driving current up in the coil in the usual fashion of a parallel resonant LC circuit.

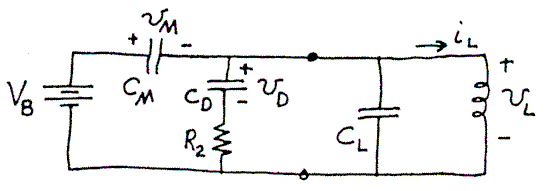
Figure 7 - A lumped component model of a coil circuit.

Analysis is complicated by the two diodes in the circuit.  As soon as V_L goes negative, D₁ starts to conduct, dissipating part of the stored energy in R₂ and limiting the negative voltage swing.  If the system still has enough energy stored for V_L to exceed V, on the positive cycle, then the MOSFET diode will conduct, thereby clamping the coil voltage at V_B.

From this analysis, it can be seen that the diode D₁ is not always essential to the circuit operation.  It acts to limit the negative voltage swing, which primarily protects the MOSFET from being operated in reverse breakdown or avalanche mode.  Modern MOSFETs are rather rugged and can withstand avalanche operation if the total energy dissipated is not too large. Also, it is quite possible that the inter-electrode capacitance can absorb all the initial magnetic energy without exceeding the MOSFET breakdown voltage.  The energy stored in a capacitor is proportional to the square of the voltage, so if V_B is one tenth of the breakdown voltage, C_L can store one hundred times the energy on the negative half cycle as it had before the MOSFET was switched off.  One can check this by making R₂ larger and looking at the negative swing of V_L on an oscilloscope.  If the MOSFET voltage rating is not being exceeded with a large R₂ then the diode can be removed entirely.

This leaves the built in diode of the MOSFET which could be clamping the positive swing of the coil voltage. If a symmetric swing is desired, a diode can be placed in series with the MOSFET, as shown in Figure 8.  This circuit forces all the energy supplied to the coil during the MOSFET on-time to remain in the coil until dissipated as heat.  This is the most efficient circuit and has the longest oscillatory decay.

Figure 8 - The most efficient coil circuit.

Conclusion

Power MOSFETs are quite suitable for driving small resonant transformers and Tesla coils at frequencies up to about 200 kHz.  They can also be used in tuning and optimizing larger units at reduced voltage and power levels.  The optimum on-time and cycle time of a mechanical commutator can be determined before the commutator is built, thus saving either improper operation or wasted effort.

References

[1] Motorola Power MOSFET Transistor Data Book, 1988.

[2] Corum, James F. and Kenneth L. Corum, "A Technical Analysis of the Extra Coil as a Slow Wave Helical Resonator," Proceedings of the 1986 International Tesla Symposium, pp. 2-1 - 2-24.