![]()
Class Notes: Tesla Coils and the Failure of
Lumped-Element Circuit Theory
by
Kenneth L. Corum and
James F. Corum, Ph.D.
© 1999 by K.L. Corum and J.F. Corum
"The working [of the Extra Coil] was excellent with
1/4 wave-length." Nikola Tesla, September 18, 1899
I. Introduction. Can one model the physical operation of a Tesla coil appropriately with only lumped-element circuits? If not, why not? It was pointed out long ago that, at its operating frequency, a Tesla coil is not a lumped-element induction coil. Forget the quest for "many turns of fine wire". In fact, a Tesla coil has more in common with a cavity resonator than it does with a conventional inductor. [See TCTUTOR, Corum, 1988, pp. 56-58; "Extra Coil as a Slow Wave Resonator," Proc. 1986 ITS Symposium, pp. 2:1-2:24; Industrial Electron Accelerators, by E.A. Abramyan, Hemisphere, 1988, p. 94.] With a real Tesla coil, voltage rise is neither by lumped-element transformer action (E2 = NE1), nor by induction (E2 = M di/dt), nor by simple lumped-element coupled resonance [V2 = V1×(L2/L1)½]. In all of those circuit models the current is analytically presupposed to be uniformly distributed along the wire in the coil (it's in the Neumann integral definition of inductance - see any elementary electromagnetics text) and the voltage will rise proportional to N, the turns along the coil. There are no standing waves on a lumped element circuit component. (In fact, lumped-element circuit theory inherently employs the cosmological presupposition that the speed of light is infinite, as every EE sophomore should know. See, e.g., - Electric Circuits, by J.W. Nilsson, Addison-Wesley, 1983, p. 3.)
However, a true Tesla coil (circa 1894) is a velocity inhibited slow-wave helical transmission line resonator: Vmax = S×Vmin, where S is the standing wave ratio. Voltage magnification is by standing waves. Period. No such voltages, even in the remotest degree, can be obtained by either lumped element transformers or by lumped element LC resonating circuits. This behavior of all quarter-wave resonators is well known. [See "Resonant Lines and Radio Circuits," by F.E. Terman, Trans. AIEE, July, 1934, pp. 1046-1053; Hyper and Ultra High Frequency Engineering, by R. Sarbacher and E.W. Edson, Wiley, 1943, p. 353; Networks, Lines and Fields, by J.D. Ryder, Prentice-Hall, 1949, p. 285; Electromagnetic Waves & Radiating Systems, by E.C. Jordan and K. Balmain, Prentice-Hall, 1968, pp. 227, 231.] In the following note, we will show why one needs transmission line analysis (or Maxwell's equations) to model these electrically distributed structures. Lumped circuit theory fails because it's a theory whose presuppositions are inadequate. Every EE in the world was warned of this in their first sophomore circuits course. (A pre-discharge, linear operating regime is being assumed for both lumped and distributed operation, of course.)
It makes no difference whether the coil is a cylindrical helix, a conical frustum, or a flat spiral. Tesla clearly understood the velocity-inhibited nature of spiral and helical resonators and taught that, "The length of the wire coil in each transformer should be approximately one-quarter of the wave length of the electric disturbance in the circuit, this estimate being based on the velocity of propagation of the disturbance through the coil itself." [U.S. Patent 645,576; Applied for Sept. 2, 1897] It's not the physical length of the wire but rather the velocity inhibited electrical length of the helical coil which must be quarter-wave resonant (i.e., have forward and reflected wave-interference producing a standing quarter-wave resonance). This was recognized by Tesla, and this is the meaning of the phrase ". . . this estimate being based on the velocity of propagation of the disturbance through the coil itself." (The consideration could not exist for a lumped element, obviously.) Berkeley physicist David Sloan, ("An RF High Voltage Generator," Phys. Rev., Vol. 47, 1935, pp. 62-70), did not know how to mathematically handle the inhibited velocity of propagation on the helical resonator, and a suitable engineering analysis was provided only a decade ago.
Is there any question that Tesla is speaking of a distributed transmission-line resonator? Well, if so, listen to his correspondence to the US Patent Examiner on November 15, 1897. He is explaining what happens if the resonator excitation-frequency is raised (i.e., the wavelength shortened). As every electrical engineer knows, a grounded quarter-wave transmission-line resonator possesses a Vmin at the base and a Vmax at the top. If the frequency is lowered, the structure is too short for quarter-wave resonance, and if the frequency is raised, then Vmax positions form down in the resonator. The same is true for both helical coils and spiral coils. Concerning the latter, Tesla wrote,
|
"If the transmitting and receiving coil were made longer than the quarter of the wave-length of the electrical disturbance in the wire, then the points of highest potential would not fall at the inner ends of the coils . . . as required, but nodal points would form, as the case may be, somewhere in the middle of the coils ..." [Dr. Nikola Tesla - Selected Patent Wrappers, compiled by J.T. Ratzlaff, Tesla Book Company, 1980, Vol. 1, p. 150.] |
This phenomenon is decisive. It occurs only on distributed resonators: it is impossible with any lumped circuit element! (The current has the same value at every point along a lumped-element.) To understand what is happening, consider a cylindrical helical coil of height H. The base is always forced to be a voltage node (it's grounded). The top is always a relative voltage loop at the odd quarter-wave resonances and a voltage node at the even (half-wave) resonances. These boundary conditions constrain the mode patterns on the structure (called spatial harmonics). We assert that velocity inhibited partially coherent forward and reflected RF traveling waves form interference patterns on the coil.
II. Physical Description. At the
fundamental (quarter-wave) resonant frequency there is a
Vmin at the base and the Vmax appears at H
(the top). At the next mode there's a Vmin at the base,
a Vmax appears at 1/3 H, then there's another
Vmin at 2/3 H, and, finally, a Vmax at the
top. (The structure is 3 quarter-wavelengths tall.) At the next
resonant mode there are voltage nodes at the base, 2/5 H, and 4/5 H;
and a Vmax appears at 1/5 H, 3/5 H, and at the top. (The
structure is 5 quarter-wavelengths tall.) To see the nodes sharply,
you have to be at the resonant frequencies. (The impedance is
following a circle around the Smith chart and the voltage is varying
accordingly.) We will number the modes in terms of the number of
quarter-waves on the structure: n = 4H/![]() g.
[The resonant frequencies are called "overtones" instead of
"harmonics". Only overtones that are integer multiples of the
fundamental are called harmonics. For a nondispersive
resonator the fundamental is called the first harmonic, the first
overtone is the second harmonic, the second overtone is the third
harmonic, etc. However, a helix is a frequency dispersive
resonator - the velocity factor is not a linear function
of frequency and, therefore, the overtones of the resonator are
not integer multiples of the fundamental.] At the
next overtone, the voltage nodes are at the base, 2/7 H, 4/7 H, and
6/7 H. The Vmax are at 1/7 H, 3/7 H, 5/7 H and the top.
Sketch a vertical line with 7 equidistant tick marks. Sketch heavy
dots (nodes) at 0, 2, 4, and 6. Sketch in loops with maxima at 1,
3, 5 and the top. (The structure is 7 quarter-wavelengths tall.)
The magnitude distribution of the spatial interference pattern is
called a standing wave. At all the odd resonant overtones, there is
always a Vmax at the top and a Vmin at the
base. The pipe organ, trombone, violin, harp, guitar, xylophone,
. . . (even a flag pole) . . . are all transmission line resonators. No
wonder Helmholtz and Lord Kelvin were so entranced by Tesla's
wonderful coil: it's a musical instrument whose very soul has been
tuned for creating an electrical fountain of celestial fire. One
can write analytical expressions for all this, of course. (They're
in Appendix VI of our book Vacuum Tube Tesla Coils.)
g.
[The resonant frequencies are called "overtones" instead of
"harmonics". Only overtones that are integer multiples of the
fundamental are called harmonics. For a nondispersive
resonator the fundamental is called the first harmonic, the first
overtone is the second harmonic, the second overtone is the third
harmonic, etc. However, a helix is a frequency dispersive
resonator - the velocity factor is not a linear function
of frequency and, therefore, the overtones of the resonator are
not integer multiples of the fundamental.] At the
next overtone, the voltage nodes are at the base, 2/7 H, 4/7 H, and
6/7 H. The Vmax are at 1/7 H, 3/7 H, 5/7 H and the top.
Sketch a vertical line with 7 equidistant tick marks. Sketch heavy
dots (nodes) at 0, 2, 4, and 6. Sketch in loops with maxima at 1,
3, 5 and the top. (The structure is 7 quarter-wavelengths tall.)
The magnitude distribution of the spatial interference pattern is
called a standing wave. At all the odd resonant overtones, there is
always a Vmax at the top and a Vmin at the
base. The pipe organ, trombone, violin, harp, guitar, xylophone,
. . . (even a flag pole) . . . are all transmission line resonators. No
wonder Helmholtz and Lord Kelvin were so entranced by Tesla's
wonderful coil: it's a musical instrument whose very soul has been
tuned for creating an electrical fountain of celestial fire. One
can write analytical expressions for all this, of course. (They're
in Appendix VI of our book Vacuum Tube Tesla Coils.)
III. An Experimental Test. In spite of the fact that Tesla, himself, concurs, all the above are just assertions until an experiment is conducted. Well, here is a simple test to see if your Tesla Coil is operating as a lumped circuit or a distributed circuit, i.e. - to see if it's possible to use lumped circuit theory to analytically model your coil. Stand your resonator up (in monopole fashion), connect a signal generator between its base and ground (you could connect the base directly to ground and link couple the generator to the coil), and sweep the oscillator up through the resonant frequencies. Hold an oscilloscope probe near the top and make a note of the frequencies (resonances) that show a Vmax. If other loop (Vmax) and node (Vmin) positions form down the coil at the higher resonant frequencies - congratulations. You're beholding a transmission line resonator. You'll see the voltage loop and node positions move down as the frequency is raised. (You could, if so disposed, measure the current along the coil. There will be a current maximum at the base and a current minimum at the top of a distributed resonator:the current entering one end of a tuned transmission line resonator is not equal to that exiting at the other end - this isn't DC!)] If either the current diminishes at the top of the coil or the loops and nodes migrate down the coil, then you have a distributed element, and lumped circuit modeling fails. Period. Lumped circuit theory isn't absolute truth, it's only an analytical theory - and in these resonators we have the case where this sophomore theory fails experimentally. The engineer must either use Maxwell's equations or distributed elements to model reality. (If lumped analysis describes your coil, cheer up - modify its operation to an open resonator and you'll see what Tesla called, on July 11, 1899, "a beautiful advance in the art"!) Helical resonators of this genre are common knowledge in the engineering community. Top loading by a sphere or toroid will foreshorten the resonator in a predictable way. (TCTUTOR, p. 50) The procedure given by Tesla is to select a top loading (toroid or sphere) that is physically large enough to prevent discharge prior to reaching the desired potential, and then design the resonator to operate with this load reactance at a frequency that brings the top-loaded system into resonance at the desired potential. (CSN, July 11, 1899) This is different than designing resonant lumped element systems, where currents are uniform along coils and voltage rises are much smaller. It was documented (analytically and experimentally) over a decade ago, and it's astonishing that it's still disputed seriously by some Tesla aficionados.
As with all experiments, be careful to control stray effects such as the mutual capacitance between the scope probe leads and the resonator. (You're looking for spatial variations in a geometrically compact field distribution.) Even the experimenter's body will modify the resonator's voltage distribution. We constructed a sliding coax-fed E-field probe. (It's a variation of the conventional slotted-line experiment so familiar to undergraduate EEs.) This simple probe samples the resonator's external E-field (proportional to the voltage distribution along the coil) without seriously perturbing the fields, and it avoids errors that would arise from the experimenter waving his arms near the coil. (An H-field probe could be used, if desired.) A simple procedure (we'll call it Test I) to observe transmission line modes on a Tesla Coil is:
|
1. Tune to the fundamental frequency and observe the Vmax at the top and the Vmin at the base. 2. With an oscilloscope probe (or even a neon bulb) near the top, tune to the first overtone (the next frequency where the Vmax at the top again reappears sharply). Then move the probe downward along the coil. You will see a Vmin (near the 2/3 H point) and a Vmax (near the 1/3 H point). And then, of course, a Vmin again at the base. [Lumped element coils can't do this.] 3. To convince yourself that the transmission line resonator theory is really gospel, tune to the 5th Vmax observed at the top (counting the fundamental as 1). The structure is then 9 quarter-wavelengths tall. There will be 5 Vmaxs, with a guide quarter-wavelength equal to the coil length divided by 9. You can either move the probe up and down the coil to find the 5 separate voltage maxima, or you can place the probe 1/9 up and swing through the Vmax. (Place the probe 2/9 up and you'll sweep through a voltage null at the same frequency.) |
[There is even enchantment for the analytically minded. If you solve Maxwell's equations on a helix for the interior and exterior fields, and match the boundary conditions radially across the helix, you will be led to a transcendental equation which must be solved iteratively for the guide phase constant from which the all important inhibited velocity factor may be determined. (It will be on the order of 1/1000 or less for a Tesla helix.) The spatial "wavelength compression factor" for the helical transmission line resonator then follows, as do the predicted resonant frequencies and the Vmax positions. This all sounds complicated, but it's not, really. And, no - there is no violation of the equation of continuity (i.e., conservation of charge) on helical resonators - even though the current is different at the two ends (the base and the top).]
We ran the experiment on the coil shown in Photo 1, below. The geometrical parameters of the coil were as follows: N = 317 turns, D = 24.3", H = 55.4", #10 gauge stranded copper (1 kV insulation), dW = 0.1019", s = 0.175". The predictions and measured data were:
Mode Predicted Vmax Measured Vmax Predicted Measured Error
Position Position fo (kHz) f (kHz) (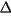 f/fo)
1 55.4" Top (55.4") 180 175 2.8%
3 18.5" 18.0" 455 435 4.4%
5 11.1" 11.0" 677 645 4.7%
7 7.9" 8.0" 903 860 4.8%
f/fo)
1 55.4" Top (55.4") 180 175 2.8%
3 18.5" 18.0" 455 435 4.4%
5 11.1" 11.0" 677 645 4.7%
7 7.9" 8.0" 903 860 4.8%
The normalized measured voltage wave interference patterns for the first three resonant frequencies were plotted alongside the coil as shown in Photo 1. The experiment was also conducted on a small helical coil with the following parameters: N = 532 turns, D = 6.3", H = 25", #18 gauge enameled, dW = .0403, s = .047". The data are tabulated below and provide added confirmation of the transmission line resonator theory.
Mode Predicted Vmax Measured Vmax Predicted Measured Error
Position Position fo (kHz) f (kHz) (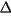 f/fo)
1 25" Top (25") 540 520 3.7%
3 8.33" 8.0" 1,210 1,240 2.5%
5 5.0" 5.0" 1,753 1,800 2.7%
7 3.6" 3.5" 2,250 2,350 4.4%
9 2.78" 2.75" 2,750 2,800 1.8%
f/fo)
1 25" Top (25") 540 520 3.7%
3 8.33" 8.0" 1,210 1,240 2.5%
5 5.0" 5.0" 1,753 1,800 2.7%
7 3.6" 3.5" 2,250 2,350 4.4%
9 2.78" 2.75" 2,750 2,800 1.8%
The theory and experiment agree to within 5%, which is acceptable engineering accuracy. Anybody should be able to obtain similar results.
IV. What's Going On? All those handbook formulas that people use for inductance, L, inherently assume applications at frequencies so low that the current distribution along the coil is uniform. (They were all derived from the Neumann integral with an assumed uniform current, which, historically, is an attempt to geometrically characterize a coil in terms of a ratio of magnetic flux linkage to impressed current.) The real issue is that migrating voltage nodes and loops are not a property of lumped-circuit elements - they are the directly observable consequence of velocity inhibited wave interference on the self-resonant coil. Lumped element representations for coils require that the current is uniformly distributed along the coil - no wave interference and no standing waves can be present on lumped elements. The problem has been that many experimenters working with self-resonant helices have pursued the concept of coil self-capacitance without really understanding where the notion comes from or why it was ever invoked by engineers. For that, they will have to go read R.W.P. King's wonderful old book Electromagnetic Engineering, McGraw-Hill, 1945. (See pp. 418-422, 461-466.) On pg. 465, the Harvard Professor points out that, for coils whose wire length exceeds 1/6 wavelength (as is the case for the secondary of authentic Tesla coils), "an adequate representation of the reactance of a coil with a nonuniformly distributed current is not possible in terms of a coil with a uniform current [a lumped-element inductance] connected in parallel with a lumped capacitance." Period. Resonant fields present surprises to engineers with limited training.
|
V.
Discussion. Figure 1 shows an actual physical system
and two candidate models: (1) a transmission line (distributed
element) model (that allows one to include the effect of a
spatially varying current distribution); and (2) a
lumped-element model. Depending upon whether you're operating
at a frequency where the current is sinusoidally distributed
along the coil or operating at a low enough frequency so that
the current is uniformly distributed along the coil, either
model may be appropriate. (Distributed theory encompasses
lumped circuits and always applies.)
In the transmission line resonator model, the ball
on the top serves as a load reactance conjugate to the
transmission line back impedance to bring the system, of
electrical length
|
 |
|
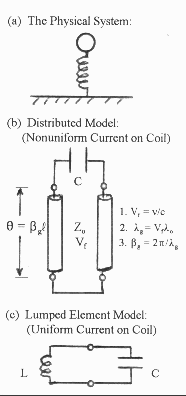
Figure 1. Physical System and Models. |
In the lumped element model, the sphere
serves as a conjugate reactance, equal and opposite to 2![]() foL,
where L is the self inductance of the coil measured at (or
calculated for) frequencies so low that the current distribution
on the coil is uniform. A thorough analytical investigation of
such tuned coupled lumped resonance was given in
TCTUTOR (p.16-44). In the lossless case, the voltage across
the secondary is given by the conservation of energy expression V2 =
V1(L2/L1)½ =
V1(C1/C2)½, RF magic
which Tesla had discovered at his Grand St. Laboratory in 1891 and
disclosed to Hertz at Bonn in 1892. (See Vacuum Tube Tesla
Coils, Appendix X.) This is the most lumped elements can give -
even if the coil has no resistance whatsoever! When real world
losses in the coil are included the voltage step-up is even smaller
than this optimistic (C1/C2)½ expression. The voltage
magnification in coupled tuned coils is nowhere near what is
possible from a simple distributed resonator with standing waves.
foL,
where L is the self inductance of the coil measured at (or
calculated for) frequencies so low that the current distribution
on the coil is uniform. A thorough analytical investigation of
such tuned coupled lumped resonance was given in
TCTUTOR (p.16-44). In the lossless case, the voltage across
the secondary is given by the conservation of energy expression V2 =
V1(L2/L1)½ =
V1(C1/C2)½, RF magic
which Tesla had discovered at his Grand St. Laboratory in 1891 and
disclosed to Hertz at Bonn in 1892. (See Vacuum Tube Tesla
Coils, Appendix X.) This is the most lumped elements can give -
even if the coil has no resistance whatsoever! When real world
losses in the coil are included the voltage step-up is even smaller
than this optimistic (C1/C2)½ expression. The voltage
magnification in coupled tuned coils is nowhere near what is
possible from a simple distributed resonator with standing waves.
VI. Operating Regimes. How can you tell whether your Tesla coil is operating in Tesla's pre-1894 tuned lumped element regime or in his post-1894 distributed resonator regime? You could just look at the field distributions, as described in the test above. Here's a decisive set of quantitative measurements to see how bad the lumped-element model really is. Do the experiment on your Tesla coil. We'll call it Test II.
| Step 1. With the sphere (or toroid) attached
on the top of your coil and a ground connected to its
base, link couple a signal generator into the bottom of
the coil and hold up an oscilloscope probe in the vicinity of
the sphere - but not so close as to interfere with the
experiment. Sweep the signal generator until the first
Vmax is observed. Call this the system resonant
frequency, fo.
Step 2. With the coil disconnected, but
the top capacitor supported at the same height above ground as
when it's on the coil, measure C.
Step 3. Calculate the capacitive reactance
of the top capacitor at the measured system resonant frequency
fo: XC(fo) = 1/(2 |
Well . . . What frequency did you get in step 5? Is it the same as fo? Is the difference within engineering accuracy, i.e. is |f-fo|/fo ×100% less than 5%? If the answer is yes, then you may confidently use lumped-element modeling. However, if the answer is no, then, from the halls of Valhalla, old Wotan, himself, is thundering out over the battlements, "#*@&%!! . . . Thor, you dumdum! You can't use lumped circuit modeling! . . ." [The coil has standing waves and is behaving as a distributed resonator.] Now, which model describes the operation of your coil? We took the coil shown in Photo 1 and top-loaded it with a 25 pF (22" by 8") toroid and performed Test II. The results were:
| Step 1. fo = 135 kHz (The
toroid load lowered the resonant frequency and foreshortened
the helical resonator to
|
By the way, TCTUTOR predicts that, for C = 25.6 pF, the operating frequency will be at f = 140 kHz, and the error is only 3.7%.
About a decade ago, while one of the authors was serving as a Senior Research Scientist at the Battelle Memorial Institute's Columbus, Ohio Laboratories, he had the opportunity to acquire Bill Wysock's Tesla Technology Research Model-10 commercial Tesla Coil. (See TCBA, 1983 Vol. 2, #3 , p. 21, and the TTR website). We have the coil's parameters and measured data before us: N = 342 turns, D = 2.0', H = 97.8", dW = 0.102" (silver stranded #10), s = 0.286". The Model-10 is capped with a large 4 foot diameter spun aluminum toroid. (See Photo 2.) The results of Test II, to determine the appropriateness of "lumped-element" coil modeling, are as follows:
| Step 1. fo = 140 kHz (measured) Step 2. C = 48 pF (measured) The 4 foot diameter toroid is supported 13 feet above ground. Step 3. XC(fo) = 23,684 ohms Step 4. L = 16.3 mH (measured with an HP-4262A bridge at 1kHz) Step 5. f = 231.25 kHz. The "lumped-element assumption" has |(f - fo)|/fo ×100% = 65.2% error. . . . (Lumped circuits? . . . Not even close.) |
|
Photo 1. Coil and normalized
measured |
|
The OSU High Voltage Lab web page can be found at http://eewww.eng.ohio-state.edu/~sebo/hvlab.html. In May, 1999, the authors were pleased to visit at Ohio State with Professor Stephen Sebo, the Lab's Director, and operate the coil once again. We digress. The conclusion to be drawn from Test II is that modeling with lumped circuits is of marginal utility (it's a naive swindle!) for really comprehending any modern Tesla coil or understanding Tesla's post 1894 research. |
 |
|
Photo 2. Bill Wysock's TTR Model-10
as |
Several years ago, a numerically modeled
transient analysis of coupled lumped-element coils was published in
the AJP ("A Solid-State Low Voltage Tesla Coil Demonstrator," by D.
Bruns, American Journal of Physics, Vol. 60, 1992, pp. 797-803).
An exact mathematical analysis of the same circuitry,
including losses, had been given in TCTUTOR back in
1988 when we pointed out that a lumped analysis is appropriate only
during the duration of the primary spark (while the coupled flux is
uniform throughout the resonator), and we indicated the great
importance of controlling the primary switching epoch.
(Finkelstein's optimum k = 0.6 criteria is valid only if the spark
duration is roughly 1/(2![]() f)
where
f)
where
![]() f
is the line splitting passband broadening of the over-coupled
circuit.) That the coupled-coil, lumped-element model of Tesla
coils is physically fallacious (it doesn't predict the
three-humped spectrum that is actually observed when the spark
duration is finite) has been known since the 1911
experimental observations of Dr. Fleming. ("Some
Resonance Curves taken with Impact and Spark-Ball Discharges," by
J.A. Fleming and G.B. Dyke, Proc. of the Physical Soc., London,
Vol. 23, 1911, pp. 136-146 (see comments by Dr. Eccles and Prof.
Howe, p. 144); Also see "100 Years of Cavity Resonator Development,"
by J.F. Corum and K.L. Corum, Proc. 1990 ITS Symposium, pp.
2:1-18, Figs. 3, 4.) Needless to say, the 1992 AJP article is
little more than the simulated impulse response of an IF can - the
kind of tuned lumped coupled circuit Tesla was using before his
splendid discovery of 1894. On the other hand, if you have
been able to model your coil with a lumped-element
inductance, L, with less than 5% error, then you've been working
with a lumped, tuned, coupled-circuit (like a radio receiver IF can)
just as Tesla was doing prior to 1894, before he discovered
the true Tesla coil. [If you've got a huge capacitance on the top
then the length of wire in the secondary may be less than
f
is the line splitting passband broadening of the over-coupled
circuit.) That the coupled-coil, lumped-element model of Tesla
coils is physically fallacious (it doesn't predict the
three-humped spectrum that is actually observed when the spark
duration is finite) has been known since the 1911
experimental observations of Dr. Fleming. ("Some
Resonance Curves taken with Impact and Spark-Ball Discharges," by
J.A. Fleming and G.B. Dyke, Proc. of the Physical Soc., London,
Vol. 23, 1911, pp. 136-146 (see comments by Dr. Eccles and Prof.
Howe, p. 144); Also see "100 Years of Cavity Resonator Development,"
by J.F. Corum and K.L. Corum, Proc. 1990 ITS Symposium, pp.
2:1-18, Figs. 3, 4.) Needless to say, the 1992 AJP article is
little more than the simulated impulse response of an IF can - the
kind of tuned lumped coupled circuit Tesla was using before his
splendid discovery of 1894. On the other hand, if you have
been able to model your coil with a lumped-element
inductance, L, with less than 5% error, then you've been working
with a lumped, tuned, coupled-circuit (like a radio receiver IF can)
just as Tesla was doing prior to 1894, before he discovered
the true Tesla coil. [If you've got a huge capacitance on the top
then the length of wire in the secondary may be less than
![]() o/(2
o/(2![]() )
and, as voiced by Professor King, the current distribution could be
uniform enough so that you can represent the transmission
line as a lumped element. But, as Tesla once told his attorney,
"A large capacity and a small self inductance is the
poorest kind of circuit which can be constructed."] The
good news is: there's a whole new realm waiting for you to explore.
"Oh brave new world that has such creatures in it!"
(Tempest, V.1)
)
and, as voiced by Professor King, the current distribution could be
uniform enough so that you can represent the transmission
line as a lumped element. But, as Tesla once told his attorney,
"A large capacity and a small self inductance is the
poorest kind of circuit which can be constructed."] The
good news is: there's a whole new realm waiting for you to explore.
"Oh brave new world that has such creatures in it!"
(Tempest, V.1)
VII. Closing Thoughts. There is nothing sacred about using a sine wave generator (a finite power signal) to perform the above tests. The more sophisticated experimenter might want to repeat Test II with a broadband white noise (stochastic) source coupled to the resonator with an untuned link. Fundamental and overtone resonances can be observed with a calibrated receiver or a spectrum analyzer. Those with a knowledge of modern optics will easily recognize even richer phenomena occurring. (It can be shown that the ultimate limit in voltage rise on the coil is set by the degree of coherence of the up and back resonator waves.) While this may shatter the egos of some coilers, contrary to popular myth, the key performance parameter for a high voltage Tesla coil is not the length of the discharge (which is a function of things like input energy and primary spark duration) but, rather, the VSWR on the resonator coil - the higher the better! [It's related to the fringe "Visibility Function" for quasimonochromatic, partially coherent optical beams. (Principles of Optics, by Born and Wolf, 5th ed., p. 506.)]
The tests above are experiments that EEs have commonly performed since the '30's in undergraduate courses associated with RF electronics, and they are easily replicated with trifling effort. Concerning idealized circuit elements, Prof. Ron Scott has written that students shouldn't be "disappointed to learn that circuit theory is not real engineering." (Linear Circuits, Addison-Wesley, 1960, p. 2.) Finally, we point out that virtually all modern Tesla Coils are velocity inhibited, distributed-element, slow wave transmission line resonators. Those asserting the contrary simply have not done their homework. Tesla said that he discovered this striking nature of coils in 1894, "That was the first single step toward ... my magnifying transmitter." [Tesla on His Work with AC, edited by L. Anderson, Sun Publishing, 1992, p. 72.]
Perform steps 1-5 of Test II on your coil. And then do Test I, mapping the voltage distributions at the fundamental and overtones. Now go back and reread Tesla's 1897 patent application comment, above. His remarks also apply in the case when "the impressed oscillations are more rapid than the free oscillations" (Patent # 1,119,732), but that's about electric fire-balls and is enchantment for another time.
Jim Hardesty has made many of the Corum papers on Tesla coils available through the PV Scientific Instruments web page at www.arcsandsparks.com.
